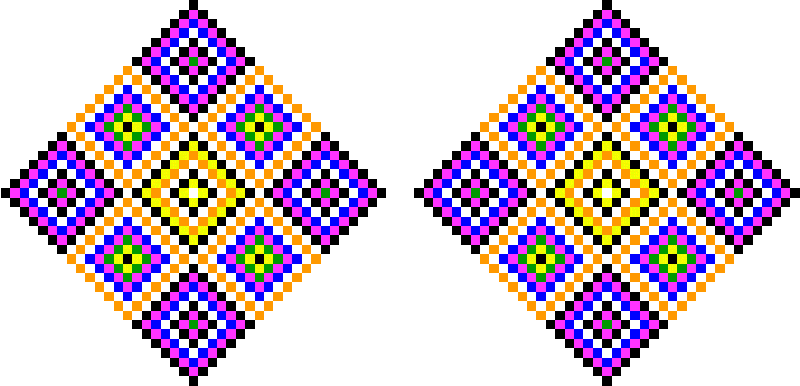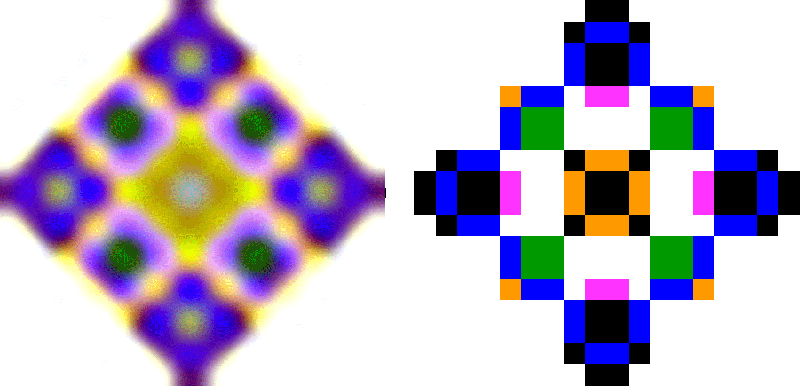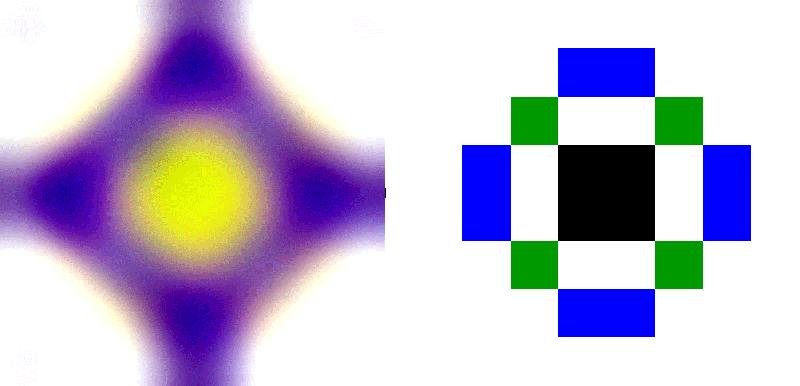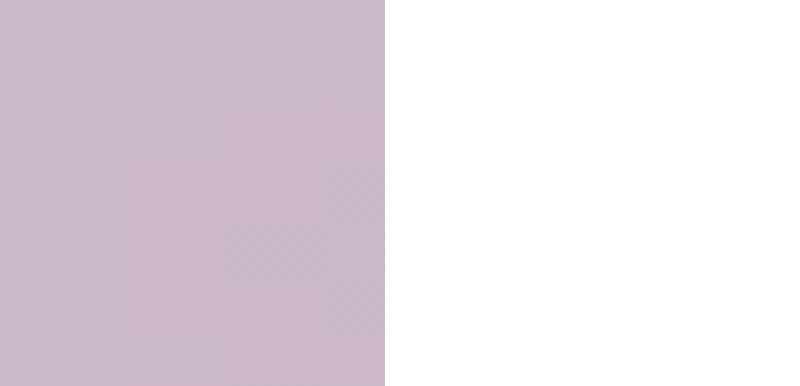http://nanoworld88.narod.ru/data/573.htm
https://subscribe.ru/archive/science.news.nanoworldnews/201803/08030328.html/
http://nanoworld.org.ru/topic/1497/
http://nanoworld.org.ru/topic/1924/page/44/
Возможно, что после восстановления фрактально упакованного (слева) изображения получится геодезическая шкала, показанная справа. Ключевым моментом является то, что после распаковывания фрактальной геодезической шкалы на ней видны мелкие деления, которых не было бы видно, если шкала не была бы фрактально упакована. Учитывая, что алгоритм распаковки работает быстро, мелкие деления можно видеть в реальном времени.
Геодезист может видеть мелкие деления, которые он не смог бы увидеть с помощью оптики на неупакованной геодезической шкале.

Орнамент звездолёта может быть не только источником энергии и двигателем, но и фрактально упакованной геодезической шкалой, состоящей из элементов-эталонов.
Более того, глядя в геодезические окуляры можно видеть 3D разметку, восстановленную после фрактальной распаковки шкалы, размещённой на стенах звездолёта. Это сильно упрощает строительство тех же мегалитов.
Строители мегалитов могли работать в системе дополненной реальности, восстановленной по нанесённой на стенах звездолёта упакованной 3D-разметке.
Только сегодня люди ещё не догадались разместить фрактально упакованную 3D разметку на стенах транспортного средства, вокруг которого можно по этой разметке строить .
Зачем нужно наблюдать мелкие деления, если окружающие объекты на таком расстоянии всё равно кажутся размытыми?
Это нужно, например, для быстрого определения линии, проходящей через точные деления геодезических рулеток, находящихся на разных расстояниях от геодезиста. Достаточно совместить восстановленные мелкие деления, и оптическая ось прибора окажется на искомой линии.
Мы предполгагаем, что это аналог матрицы Серпинского для "аппаратного" сжатия изображения.
О модели случайного блуждания на ковре Серпинского*
Н.С. АРКАШОВ, Е.В. ЛЕЖНЕВ
Основы фрактального сжатия изображений
Цитата: недостаток фрактального сжатия виден невооруженным глазом. Можете сами подсчитать, сколько доменных блоков размером 32×32 содержит двухмегапиксельное изображение. Полный их перебор для каждого рангового блока и есть основная проблема такого вида сжатия — кодирование занимает очень много времени.
Декодирование же производится просто и довольно быстро. Берем любое изображение, делим на ранговые области, последовательно заменяем их результатом применения соотв. преобразования к соотв. доменной области (что бы она ни содержала в данный момент). После нескольких итераций исходное изображение станет похоже на себя:
Вот почему в инопланетной геодезии результат фрактального сжатия фиксируют "аппаратно", т.е. превращают в изделие (орнамент на фасаде храма, на обшивке звездолёта). Это позволяет экономить время. А распаковка происходит быстро.
Теперь нам осталось разобраться, как распаковывать инопланетные фракталы типа матрицы Серпинского
Интересно понять алгоритм, где за простым геодезическим маркером (на лбу) следует более сложный фрактальный маркер (на груди). Этот алгоритм из области сжатия изображений.
Модифицированная матрица Серпинского, т.е. матрица Серпинского-Кушелева получается следующим образом.
1. Замена разноцветных элементов на два контрастных цвета, например, белый и красный.
2. Поворот на 45 градусов по часовой стрелке.
3. Вычетание треугольного элемента в центральной части нижнего ряда.
4. Достраивание путем добавления зеркального изображения.
Понятно, что это та же самая матрица Серпинского-Кушелева:.
Только в ней сделана ещё одна модификация:
Матрица Серпинского-Кушелева (7 цветов и система RGBYKWO)
Вариант реконструкции матрицы Серпинского-Кушелева для системы RGBYKWO ("шахматный семицветик")
В однопиксельном формате
Одномерная шкала
Двухмерная шкала
Видимое изображение - восстановленное изображение